CMC Markets 在波動中看好實體貴金屬,在新加坡招募監管職位
CMC Markets 正在尋求擴大在新加坡的監管許可,以進入實體貴金屬市場。
摘要:資金管理是任何一次交易行為都要涉及的技術(進場交易多少頭寸、加倉多少頭寸、減倉多少頭寸、出場交易多少頭寸),正確的資金管理方式應該很簡單,一方面你的頭寸不能過大,否則會有破產的可能性(破產風險應該等於0),一方面你的頭寸不能過小,否則即使後市行情很大,你的絕對獲利還是很小。
交易高手都注重的一文,打開你的眼界
永遠不要在一筆生意上投入過多的資本。
資金管理
什麼是資金管理
資金管理是任何一次交易行為都要涉及的技術(進場交易多少頭寸、加倉多少頭寸、減倉多少頭寸、出場交易多少頭寸),正確的資金管理方式應該很簡單,一方面你的頭寸不能過大,否則會有破產的可能性(破產風險應該等於0),一方面你的頭寸不能過小,否則即使後市行情很大,你的絕對獲利還是很小。
所以資金管理幫助交易者限制風險(有效的資金管理能幫助你安然度過對每一個交易者來說都不可避免的逆境時期),同時幫助交易者提高收益,能否根據賬戶規模合理限制交易頭寸(以及根據概率行事),是做交易和賭博之間的分水嶺。
每個交易者應該用如履薄冰的態度對待自己的賬戶資金,因為賬戶虧損的難度遠低於賬戶盈利,賬戶虧損50%,需要你盈利100% 才能回到初始額度,這是何等的難度啊!

破產風險
破產風險的概念很簡單,指的是連續虧損導致破產的可能性,想像一個玩剪刀石頭布,你有100 元,輸贏一次各50,你只要連續輸兩次你就破產了,但是你每次只賭1 元,你的破產風險就接近於0 了。
我們可以通過比較複雜的數學公式來計算自己的頭寸量是否會導致破產,也可以簡單的通過瀏覽近幾十年的數據,觀察一下最大的滑點、跳空是多少,看看自己持有的頭寸是否會在這些大的跳空中導致破產。
任何使得破產風險超過0 的頭寸,都算重倉。
我們將具體介紹破產風險的具體衡量手段。三個影響破產風險的因素:
勝率、盈虧比、單筆交易風險佔總資金比例 (破產風險模型化)
遺憾的是,由於數學上的困難,破產風險無法給出一個精準的計算公式,但我們可以從影響破產風險的三個維度進行建模仿真,在交易次數足夠多的情況下,破產風險值趨於穩定。
以下為《期貨交易者資金管理策略》中的模擬結果:





結論
勝率越大,破產風險越小
盈虧比越大,破產風險越小
單筆交易風險佔總資金比例越小,破產風險越小
同時我們也要考慮到幾個交易系統的現實:
一個優質的交易系統,平均勝率在50% 上下,且較難提高;平均盈虧比較難跨越5 ,降低破產風險最有效最簡單的方法就是減少單筆交易風險佔總資金比例了,保守的交易員會把這個數值控制在3% 內,較為激進的交易員會控制在5% 內。
實際操作中哪種資金管理方式最好?
資金管理無法把一個本身沒有優勢的交易策略從虧損狀態變成盈利狀態,但是可以避免把一個本身有優勢的交易策略從盈利狀態變成虧損狀態,所以資金管理並不是一種救命藥,只是一個完整交易系統必備的組成部分,僅此而已。
正確的資金管理方式應該很簡單,一方面你的頭寸不能過大,否則會有破產的可能性(破產風險應該等於0),一方面你的頭寸不能過小,否則即使後市移動很大,你的絕對獲利還是很小。
所以資金管理幫助交易者限制風險,同時幫助交易者提高收益。
固定百分比資金管理
固定百分比資金管理是一種非常流行的方法,同時也非常穩健,她的優點在於,在虧損的時候延緩本金下降速度,而在盈利的時候加快本金上漲速度。我會建議所有個人交易員嘗試使用這種資金管理方式。
基本計算公式如下:

N% 代表單筆交易風險佔總資金比例,一般設定在5% 內。止損距離等於開倉位-止損位(可以把點差、滑點計算在內)。
免責聲明:
本文觀點僅代表作者個人觀點,不構成本平台的投資建議,本平台不對文章信息準確性、完整性和及時性作出任何保證,亦不對因使用或信賴文章信息引發的任何損失承擔責任

CMC Markets 正在尋求擴大在新加坡的監管許可,以進入實體貴金屬市場。

近期行情波動劇烈,不少投資人有布局外匯市場的打算。值得注意的是,過去這段時間外匯天眼收到許多用戶針對UNICORN PRIME LIQUIDITY這平台的投訴爆料,指控其存在詐騙行為,下面就讓我們帶大家深入了解相關內容。
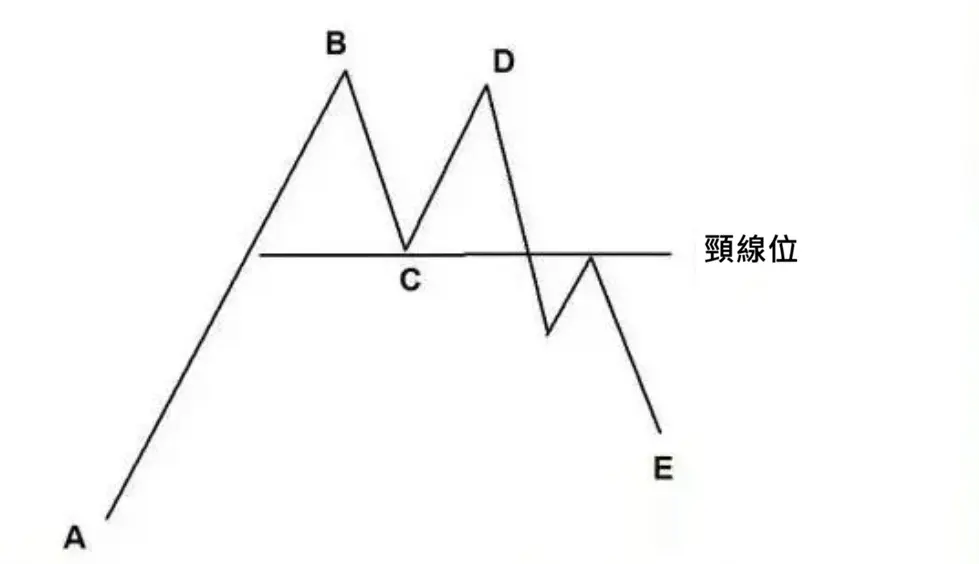
M形頂又稱雙重頂,出現在一段上漲行情的末尾,該形態有兩個明顯的價格高峰,且兩個高峰的最高點大致處於同一價位上,形狀就像是一個英文字母M。W形底又稱雙重底,出現在一段下跌行情的末尾,該形態有兩個明顯的價格低谷,且兩個低谷的最低點大致處於同一價位上,形狀就像是一個英文字母W。

剛結束農曆春節長假,不少人可能打算來點新氣象,開展新的投資。但值得注意的是,市場充斥各種詐騙平台,誆稱能提供無風險高報酬的投資標的來非法吸金。有鑑於此,外匯天眼將2/11-2/24收到的投訴與諮詢平台彙整後,整理出最新的外匯詐騙風險平台,如下:Gleneagle、Gold Fun Corporation Ltd金豐來有限公司、Theos Markets、Tongda通達國際。